Aclaremos estos conceptos erróneos porque parecen repetirse una y otra vez.
1) La ley de la potencia en sí misma no indica burbujas
Es esencial enfatizar este punto repetidamente: según el modelo de la ley de potencia, no hay burbujas inherentes. Cualquier desviación aparente (burbujas y correcciones) se anula efectivamente entre sí a largo plazo, dejando intacta la tendencia subyacente.
Las burbujas existen a un nivel más profundo y se pueden analizar
Si bien la ley de la potencia suaviza los extremos, las burbujas se manifiestan en los datos.
Al restar la tendencia general de la ley de potencia de la serie de precios, puede aislar y estudiar estas desviaciones: su estructura, patrones y regularidades.
Este enfoque basado en datos es muy superior a las conjeturas especulativas sobre futuros picos.
2) Caracterización de las burbujas:
Método de decaimiento exponencial
Existen varias técnicas para modelar estas burbujas. Un método fiable observa que el decaimiento desde los máximos máximos suele seguir un patrón exponencial. Si este decaimiento persiste, sugiere que la próxima burbuja podría desviarse aproximadamente un 80% por encima de la tendencia de la ley de potencia. Por ejemplo, si la ley de potencia proyecta un nivel de referencia de alrededor de 130K para fin de año (un punto común para los topes de ciclo), esto implica un pico potencial cercano a 200K. Alternativamente, puede visualizar esto como un "canal de decaimiento" que limita la parte superior a lo largo del tiempo.
3) Regresión cuantil para modelar desviaciones
Otro enfoque utiliza la regresión cuantílica para modelar las desviaciones de la ley de potencias. He discutido los pros y los contras de este método en detalle en uno de mis artículos (enlace en los comentarios). Su ventaja es que no requiere una suposición explícita de decaimiento para las tapas. Sin embargo, un inconveniente clave es que ajusta las leyes de potencia directamente a los picos, lo que puede sobrestimar las posibles desviaciones.
Es por eso que modelos como @TheRealPlanC
tienden a predecir máximos más altos en comparación con los míos.
4) Modelo de cuantiles híbridos con decaimiento
Para abordar las limitaciones, puede mejorar el método cuantílico incorporando un componente de decaimiento explícito, como se describe en mi artículo. Este híbrido combina las fortalezas del canal de decaimiento (delimitación realista de picos) y la regresión cuantílica (manejo flexible de distribuciones de datos), lo que produce estimaciones más equilibradas.
5) Crítica al enfoque de Bitbo (ley de potencia ajustada a tops o el corredor de la ley de potencia)
El método Bitbo simplemente ajusta una ley de potencia directamente a través de los máximos históricos, una idea propuesta por primera vez por @hcburger1 para estimar rangos potenciales (llamó a esto el Corredor de la Ley de Potencia). La parte inferior del corredor, por cierto, es válida y está respaldada por estadísticas sólidas. Pero no la cima.
Si bien he discutido esto con él extensamente, no es el enfoque óptimo: es similar a la regresión cuantílica, pero inferior, ya que asume que una simple ley de potencia gobierna la parte superior.
En realidad, solo el percentil 50 inferior de los datos se adhiere estrictamente a una ley de potencia; Las tapas exhiben un comportamiento más complejo. Esto conduce a estimaciones poco fiables y exageradas.
Espero que este desglose aclare las distinciones entre estos métodos.
En general, recuerde que las predicciones de las desviaciones de la burbuja son inherentemente menos predecibles que la propia tendencia de la ley de potencia central. La ley de potencias sigue siendo sólida y se fortalece con más datos, sirviendo como referencia fundamental.
Las desviaciones específicas del ciclo, si bien son útiles, son secundarias y no centrales para la teoría: se basan en la ley de potencia para el contexto y conllevan una mayor incertidumbre.
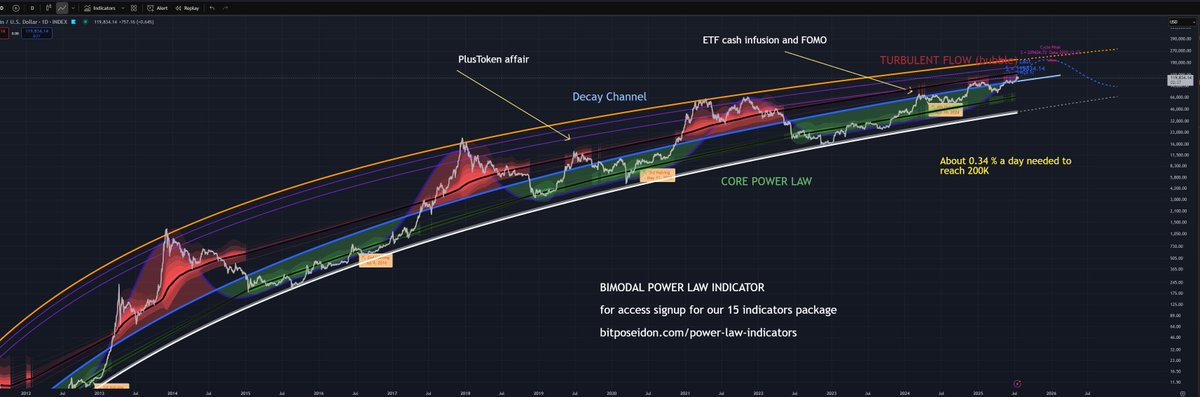
¿Cómo puede la ley de potencias tener alguna legitimidad cuando tres modelos separados de ley de potencias pueden llegar a bandas superiores YE25 que varían en un 150%?
@BitboBTC: 500 mil dólares
@TheRealPlanC: $350K
@Giovann35084111: $200 mil
16.38 k
90
El contenido al que estás accediendo se ofrece por terceros. A menos que se indique lo contrario, OKX no es autor de la información y no reclama ningún derecho de autor sobre los materiales. El contenido solo se proporciona con fines informativos y no representa las opiniones de OKX. No pretende ser un respaldo de ningún tipo y no debe ser considerado como un consejo de inversión o una solicitud para comprar o vender activos digitales. En la medida en que la IA generativa se utiliza para proporcionar resúmenes u otra información, dicho contenido generado por IA puede ser inexacto o incoherente. Lee el artículo enlazado para más detalles e información. OKX no es responsable del contenido alojado en sitios de terceros. Los holdings de activos digitales, incluidos stablecoins y NFT, suponen un alto nivel de riesgo y pueden fluctuar mucho. Debes considerar cuidadosamente si el trading o holding de activos digitales es adecuado para ti según tu situación financiera.


