Your gateway to crypto trading is just a click away
Open an account in minutes
Sign up, verify, and deposit to start your crypto journey today
Build your portfolio
Whether you’re a seasoned professional or just starting out, our platform offers the tools and resources you need to access a range of digital assets with ease
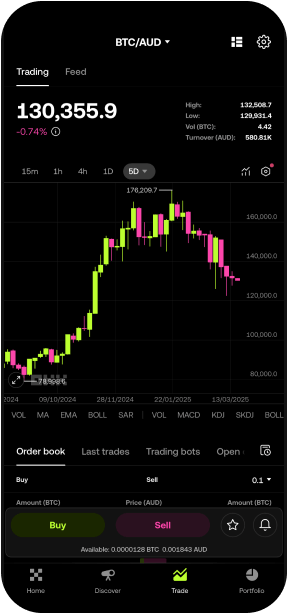
Buy cryptoComplete your favourite trades with competitive fees in Australia
One platform — unlimited possibilities. Get low fees, high-speed transactions, powerful APIs, and more.
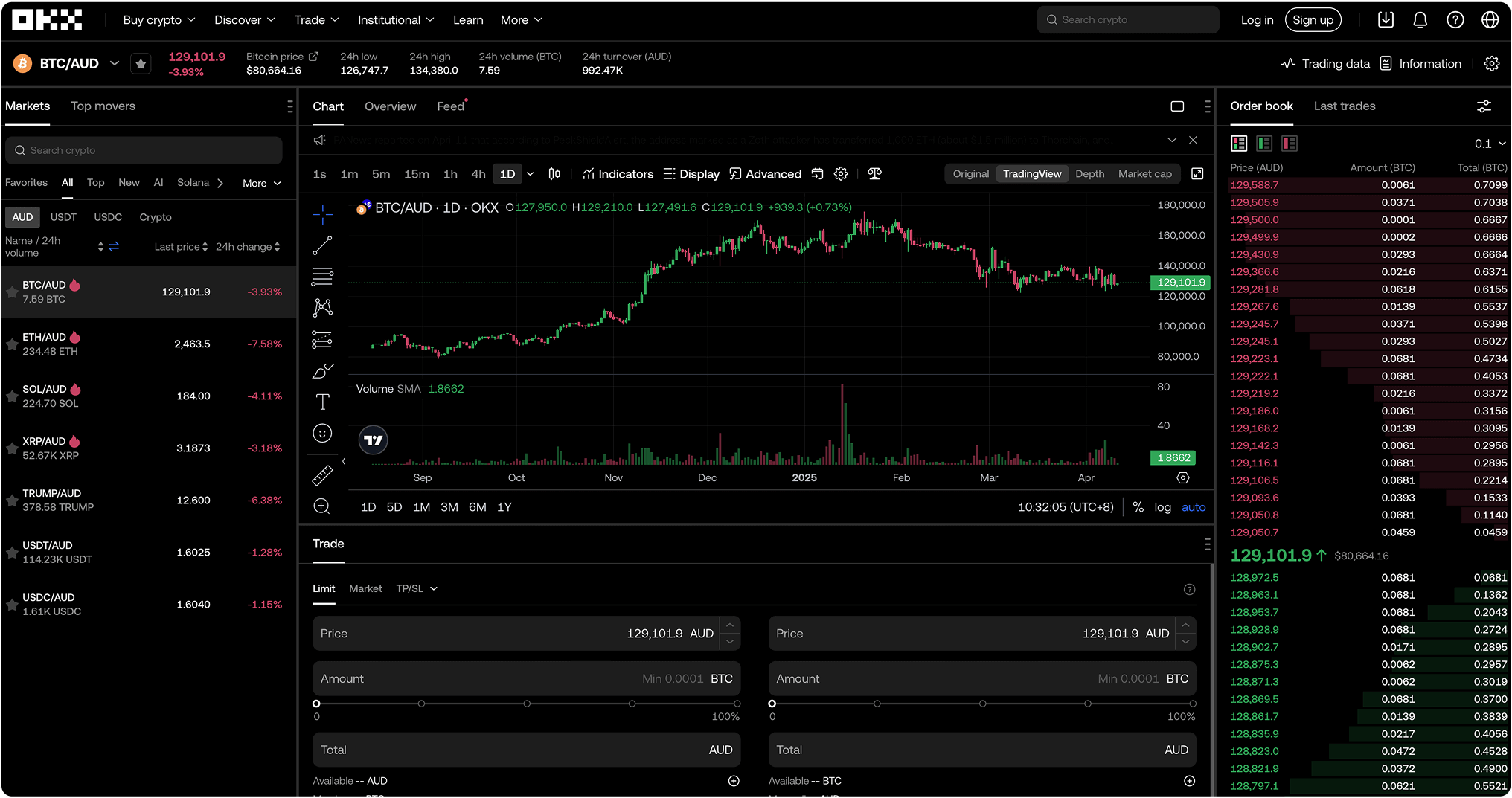
With you every step of the way
From making your first crypto trade to becoming a seasoned trader, you’ll have us to guide you through the process. No question is too small. No sleepless nights. Have confidence in your crypto.
Coach Pep Guardiola
Explains “crazy football formation”
Rewrite the system
Welcome to Web3
Snowboarder Scotty James
Brings in the whole family
Questions? We’ve got answers.
What products does OKX provide in Australia?
Do I have to be in Australia to use OKX?
Why should I trust OKX Australia?
Is OKX licensed in Australia?
How can I apply for access to derivative products on OKX?