让我们澄清这些误解,因为它们似乎一再重复。
1) 幂律本身并不表明存在泡沫
必须反复强调这一点:根据幂律模型,没有固有的泡沫。任何明显的偏差(泡沫和修正)在长期内实际上会相互抵消,保持基础趋势不变。
泡沫在更深层次上存在,可以进行分析
虽然幂律平滑了极端情况,但泡沫确实在数据中表现出来。
通过从价格序列中减去整体幂律趋势,您可以孤立并研究这些偏差——它们的结构、模式和规律。
这种数据驱动的方法远胜于对未来峰值的投机性猜测。
2) 特征化泡沫:
指数衰减法
有几种技术可以建模这些泡沫。一种可靠的方法观察到,从峰值高点的衰减通常遵循指数模式。如果这种衰减持续存在,则表明下一个泡沫可能会偏离幂律趋势约80%。例如,如果幂律预测年末的参考水平约为130K(周期顶部的常见点),这意味着潜在的峰值接近200K。或者,您可以将其可视化为一个“衰减通道”,在时间上限制顶部。
3) 用分位数回归建模偏差
另一种方法使用分位数回归来建模与幂律的偏差。我在我的一篇文章中详细讨论了这种方法的优缺点(链接在评论中)。它的优点是它不需要对顶部进行明确的衰减假设。然而,一个关键的缺点是它直接将幂律拟合到峰值,这可能会高估可能的偏差。
这就是为什么像@TheRealPlanC的模型往往预测比我的模型更高的顶部。
4) 带衰减的混合分位数模型
为了解决局限性,您可以通过结合明确的衰减组件来增强分位数方法,如我在文章中所述。这种混合模型结合了衰减通道(对峰值的现实限制)和分位数回归(灵活处理数据分布)的优点,从而产生更平衡的估计。
5) 对Bitbo方法的批评(幂律拟合顶部或幂律走廊)
Bitbo方法只是直接通过历史顶部拟合幂律,这是@hcburger1首次提出的想法,用于估计潜在范围(他称之为幂律走廊)。顺便说一下,走廊的底部是有效的,并得到了坚实的统计支持。但顶部则不是。
虽然我与他进行了广泛的讨论,但这并不是最佳方法——这类似于分位数回归,但劣于它,因为它假设简单的幂律支配顶部。
实际上,只有数据的下50百分位严格遵循幂律;顶部表现出更复杂的行为。这导致不可靠和夸大的估计。
我希望这个分析能澄清这些方法之间的区别。
总体而言,请记住,泡沫偏差的预测本质上比核心幂律趋势本身更不可预测。幂律仍然是稳健的,并随着数据的增加而增强,作为基础参考。
特定周期的偏差虽然有用,但是次要的,并不是理论的核心——它们依赖于幂律作为背景,并带有更高的不确定性。
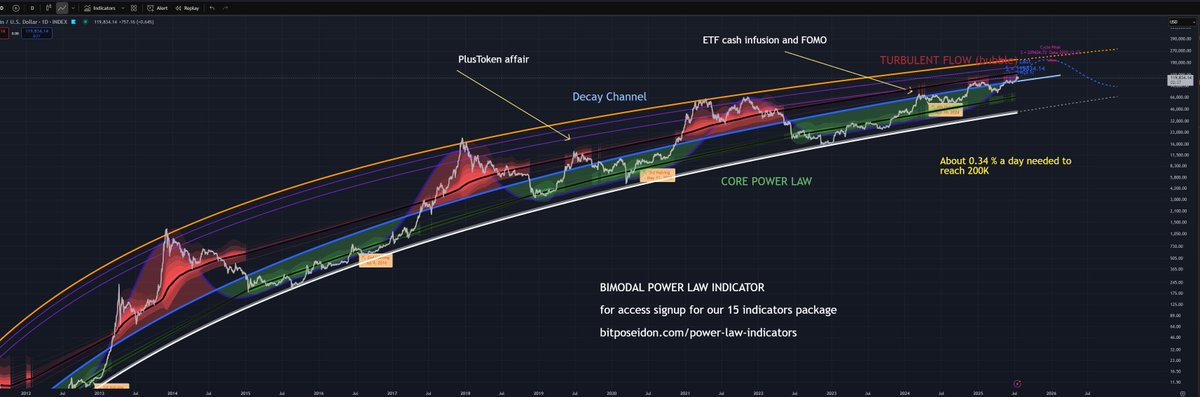
当三个不同的幂律模型得出的 YE25 上限相差 150% 时,幂律如何能有任何合法性?
@BitboBTC: $500K
@TheRealPlanC: $350K
@Giovann35084111: $200K
1.64万
90
本页面内容由第三方提供。除非另有说明,欧易不是所引用文章的作者,也不对此类材料主张任何版权。该内容仅供参考,并不代表欧易观点,不作为任何形式的认可,也不应被视为投资建议或购买或出售数字资产的招揽。在使用生成式人工智能提供摘要或其他信息的情况下,此类人工智能生成的内容可能不准确或不一致。请阅读链接文章,了解更多详情和信息。欧易不对第三方网站上的内容负责。包含稳定币、NFTs 等在内的数字资产涉及较高程度的风险,其价值可能会产生较大波动。请根据自身财务状况,仔细考虑交易或持有数字资产是否适合您。


